AGMG performance

Robustness and multithreading

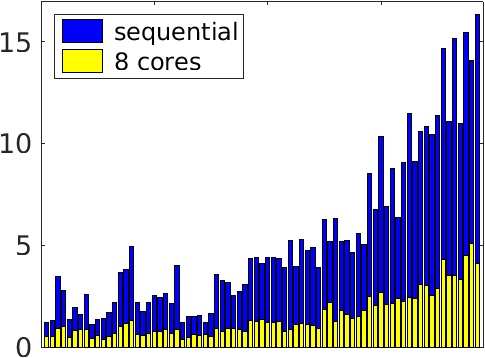
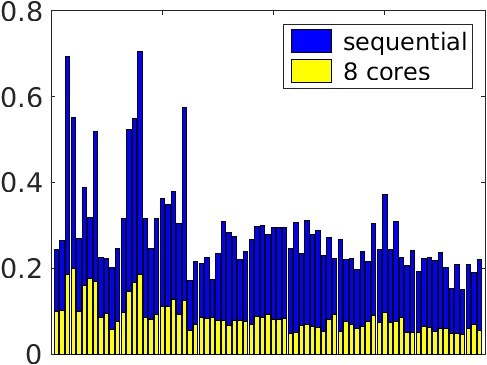
The robustness of AGMG has been assessed on a large test suite of discrete second order elliptic PDEs, comprising

problems on 2D/3D regular grids and on 2D/3D unstructured grids, some with strong local refinement

problems with (big) jumps and/or (large) anisotropy in the PDE coefficients

symmetric (positive definite) and nonsymmetric problems (2D/3D convection-diffusion problems with dominating convection based on recirculationg flow)

finite difference and finite element (up to p4) discretizations

Systems size: from 5.x10⁵ to 3.x10⁷ unknowns
Number of nonzero entry per row: from 5. to 74.

First 2 graphics: Total wall clock time to solve the linear system in microseconds per unknown or microseconds per nonzero entry in the system matrix - vs - problem index (problems ordered by increasing number of nonzero entry per row)

Performed on a desktop workstation with Intel XEON E5-2620 at 2.10GHz, 2017.

Time per unknown

Time per nonzero entry

Comparison with other solvers

AGMG has been compared against several other state-of-the-art linear system solvers; see here for technical details.

Next 8 graphics: Total wall clock time to solve the linear system in microseconds per unknown - vs - number of unknowns

Performed on a computing node with Intel XEON L5420 processors at 2.50GHz, 2012.

Pay attention that bot scales are logarithmic.

Poisson equation in a square (2D)
Finite Difference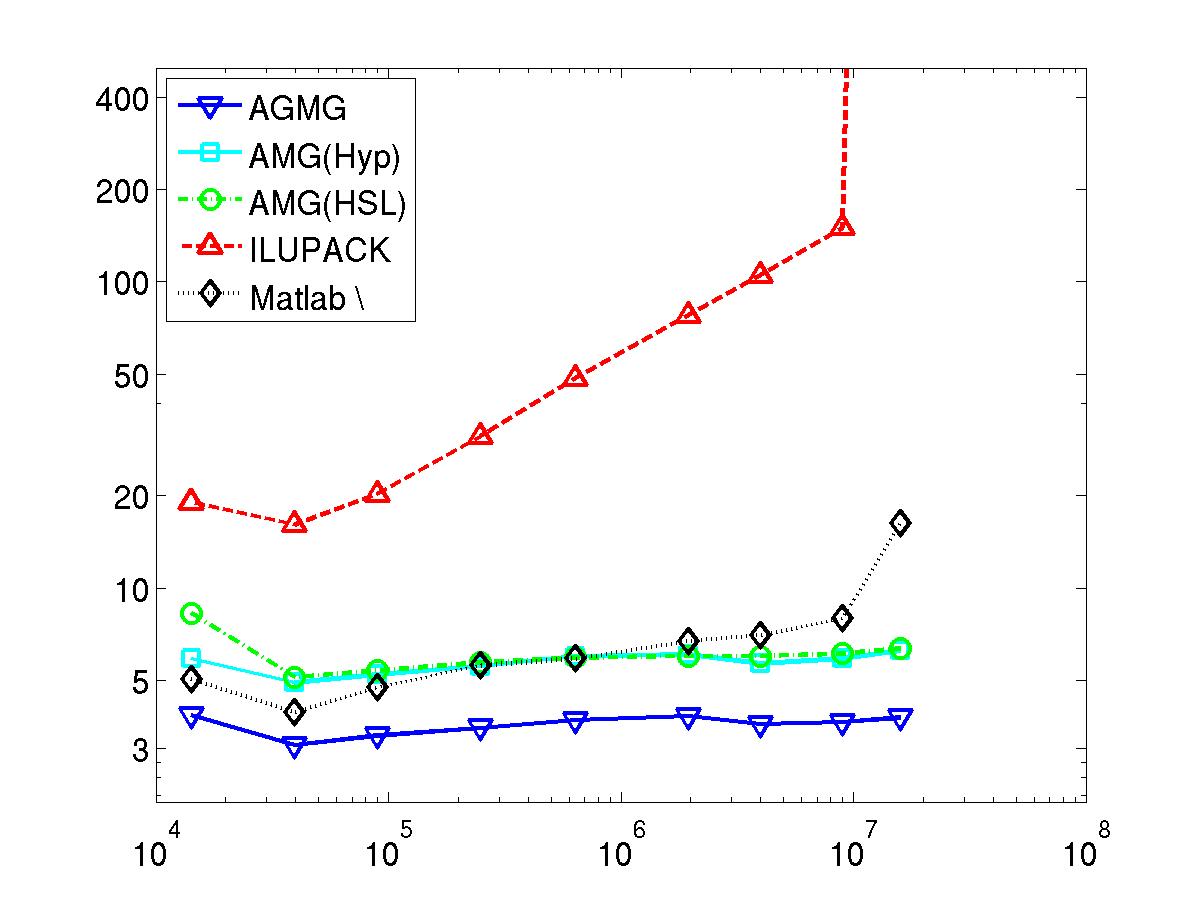

Poisson equation in a L-shaped domain (2D)
Linear Finite Element with strong local
refinement near the reentering corner

Poisson equation in a cube (3D)
Finite Difference

Poisson equation in a cube (3D)
Linear Finite Element with local refinement upon and near the
surface of a small sphere at the center of the cube

Poisson equation in a square (2D)
Cubic (p3) Finite Element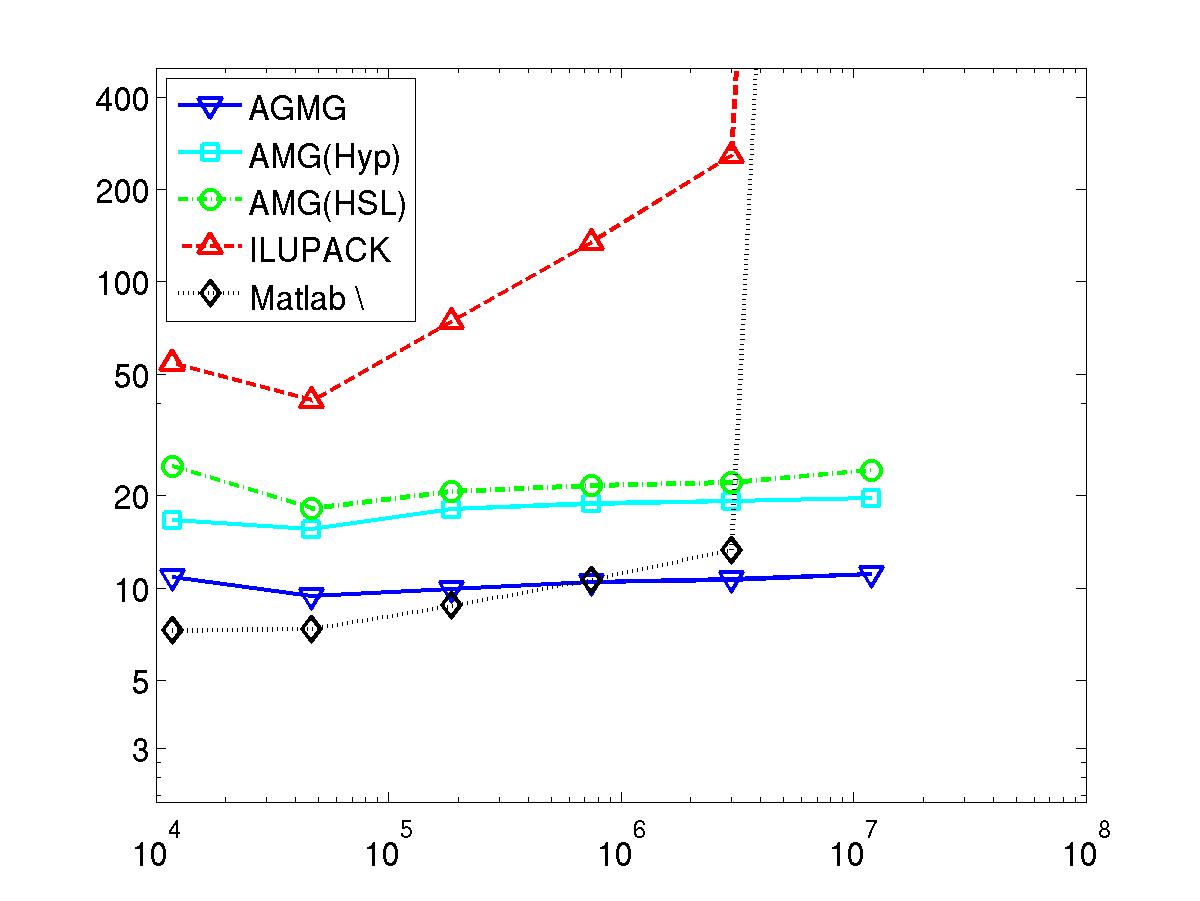

Convection-diffusion equation in square (2D)
(recirculating wind, dominating convection)
Upwind Finite Difference

Poisson equation in a cube (3D)
Cubic (p3) Finite Element

Convection-diffusion equation in a cube (3D)
(recirculating wind, dominating convection)
Upwind Finite Difference

Parallel performance

AGMG has also been tested on some truly large scale HPC systems.

Last 4 graphics: Total wall clock time in seconds to solve the linear stemming from the 7-point finite difference discretization of the Poisson equation in a cube.

For all weak scaling plots, the x-scale (problem size) is logarithmic whereas the y-scale (time) is not. Both scales are logarithmic for the strong scaling plot.

Top right figure: 373248 cores represents more than 80% of the whole machine JUQUEEN, which is ranked eighth in the top 500 supercomputer list of November 2013.

Weak scalability results on Intel Farm (CURIE, 2014):
time as a function of the number of unknowns.
(fixed problem size per core)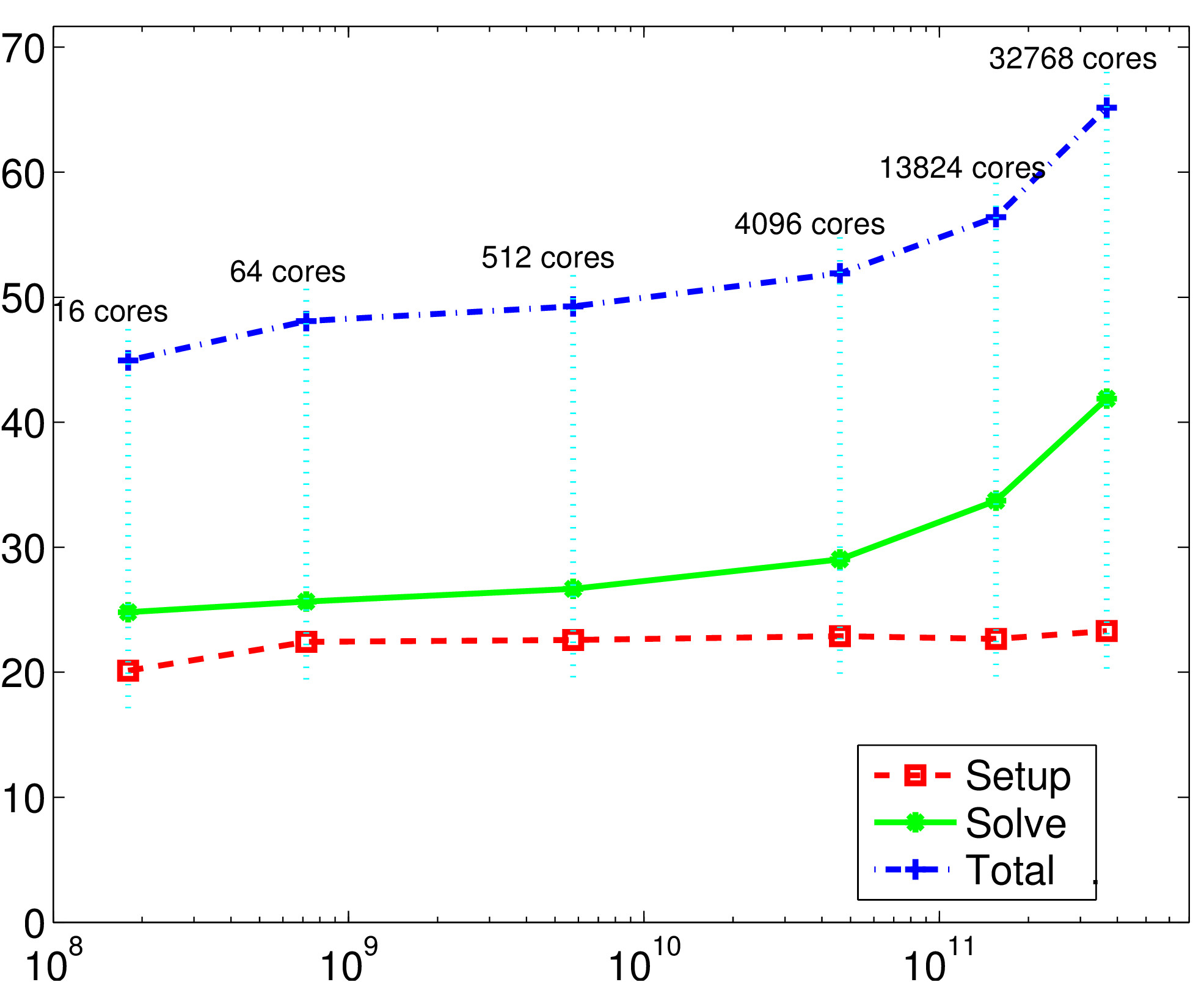

Weak scalability results on Cray XE6 (HERMIT, 2014):
   time as a function of the number of unknowns
   (for different problem sizes per core)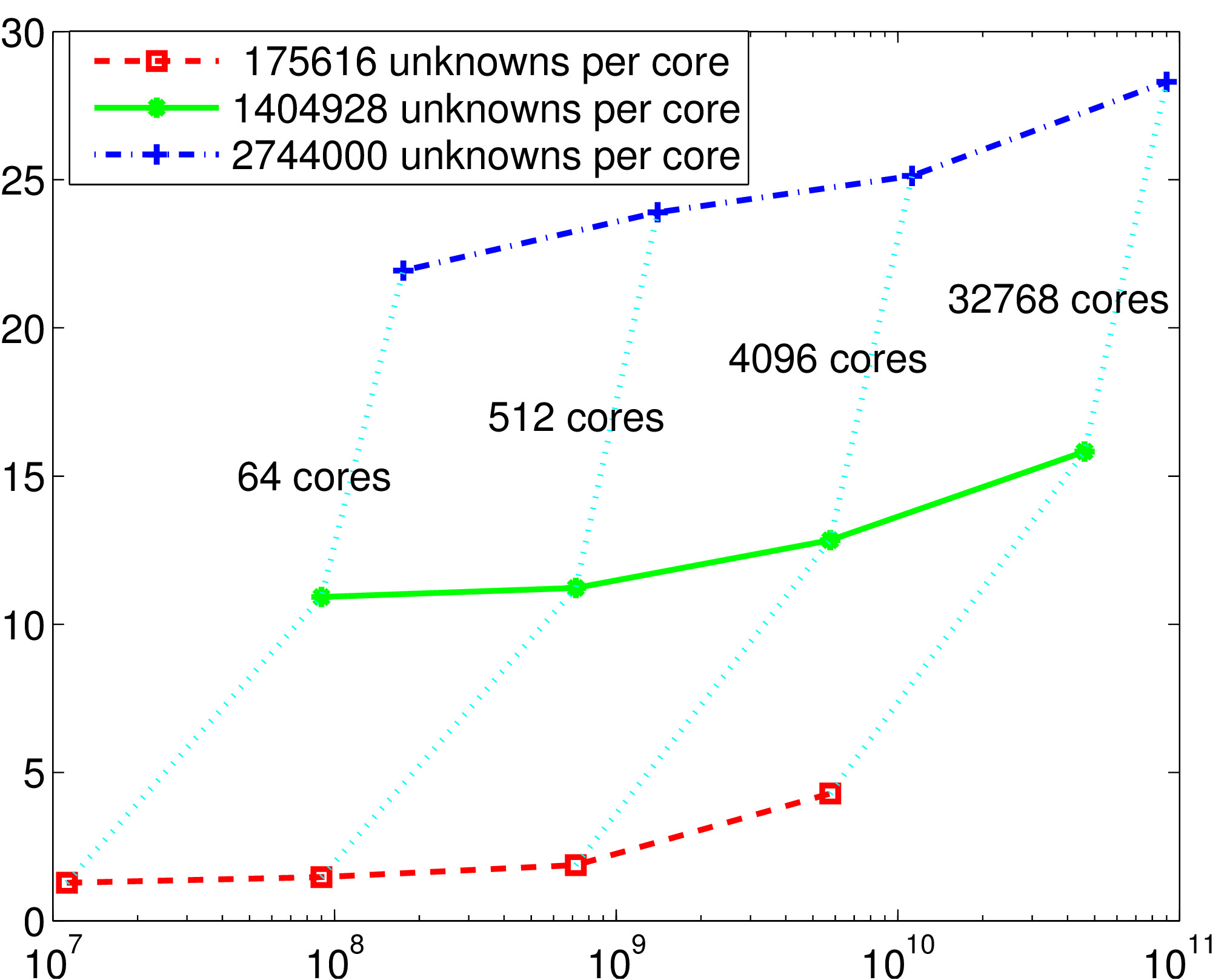

Weak scalability results on IBM BG/Q (JUQUEEN, 2014):
time as a function of the number of unknowns.
(fixed problem size per core)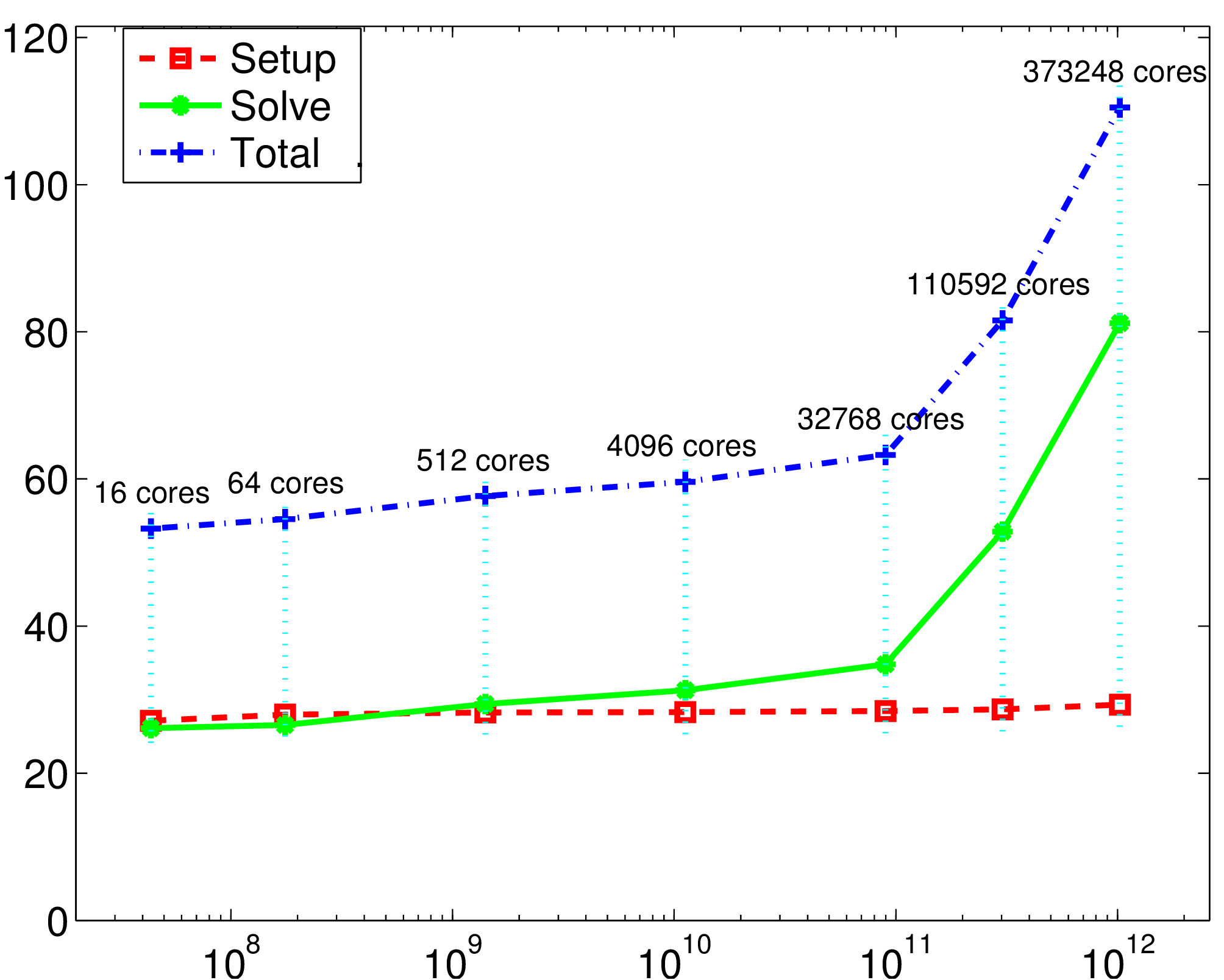

Strong scalability results on Cray XE6 (HERMIT, 2014):
   time as a function of the number of cores
   (fixed problem size: 87.5x10⁶ unknowns).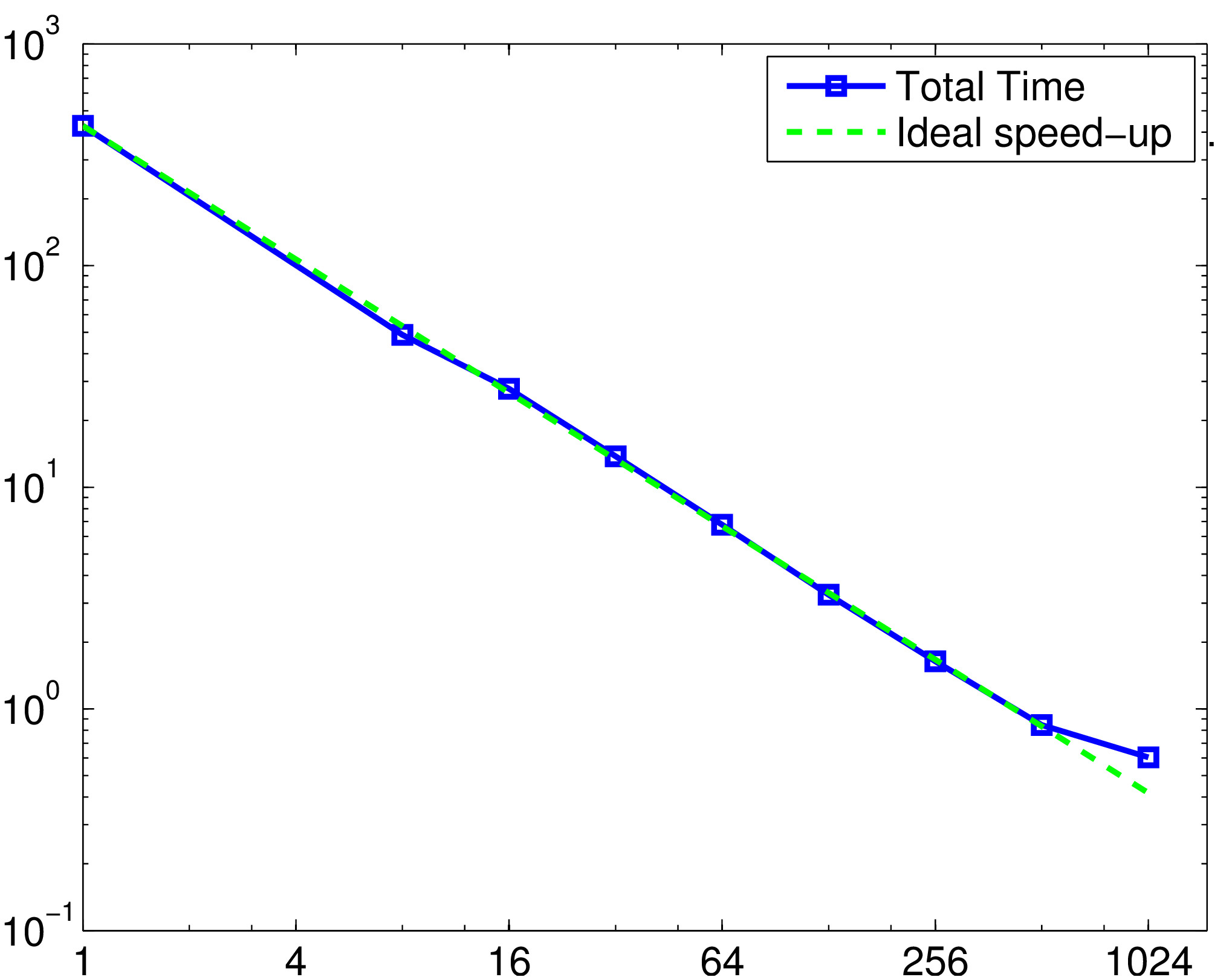

We acknowledge PRACE for awarding us access to resources CURIE (Intel farm at CEA, France), JUQUEEN (IBM BG/Q at Juelich, Germany) and HERMIT (Cray XE6 at HLRS, Stuttgart, Germany).

Contact Main AGMG page